ISIS Overview of SAS Data Analysis

Small-Angle Scattering (SAS) is a very mature investigative technique with applications in numerous different scientific areas. Consequently, the information content in the measured data can vary considerably as the following examples show.

SANS from a solid blend of h8 & d8 polystyrene: 1 P(Q)

SANS from a micellar dispersion of the surfactant SDS in water: 1 P(Q) x 1 S(Q)

SANS from a solid surfactant-templated porous material: 6 P(Q)'s

There is also a wide variety of information that can be extracted from the data depending on the approach to data analysis. Sometimes more than one of the approaches below may be useful (or even demanded) depending on factors such as the area of science, the understanding of the system(s) studied that is being sought, the users expertise and resources, or even the requirements of the intended journal.

The table below is intended as a 'signpost' to help the reader navigate these different approaches.

Model-Fitting Methods	Real-Space Methods	Ab-Initio Methods	MC/MD Methods	Other Methods
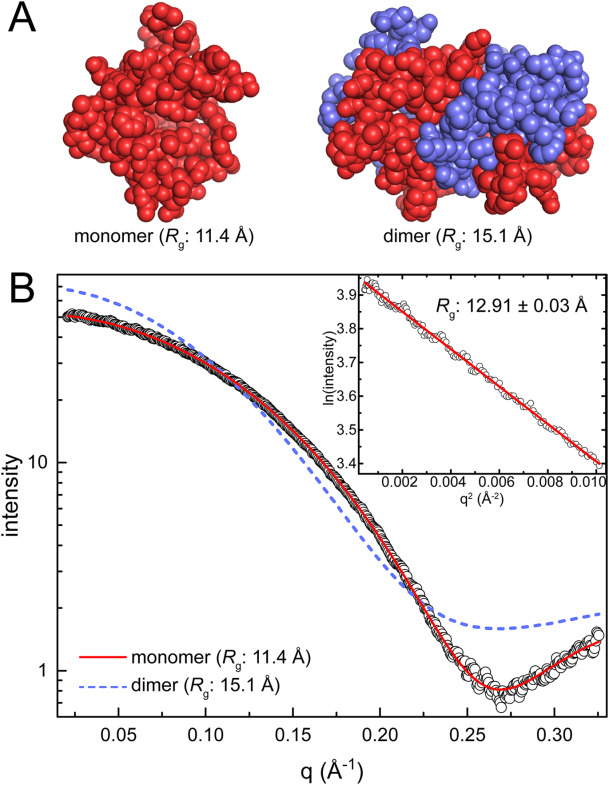
Example of 2D model-fitting using the SasView application	Cavity size distributions in a steel weldment as derived from SANS 10.1179/1743284714Y.0000000577	Ab-initio modelling of polcalcin constrained by SAXS 10.1002/pro.3376	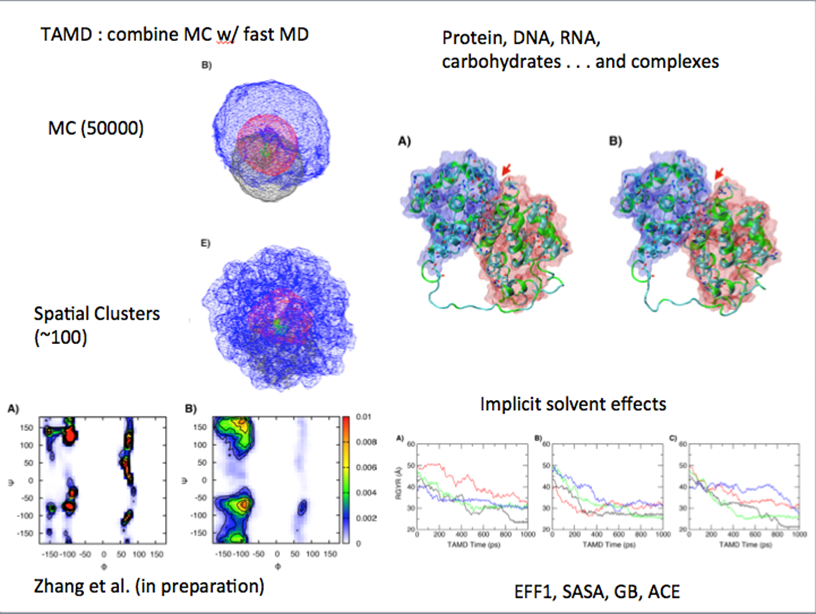MC & TAMD modelling of proteins constrained by SANS 10.1016/j.jmgm.2017.02.010	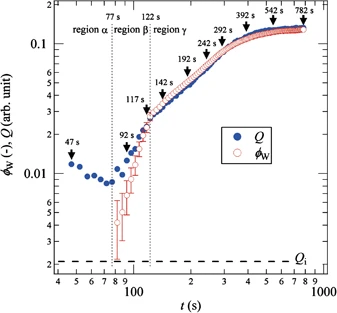Time evolution of the invariant during crystallisation of P4MP1 10.1038/pj.2012.204
This approach uses iterative optimisation to match the calculated scattering from a model function describing the scattering objects to the measured scattering data. Each iteration one or more physical parameters describing the model (e.g. concentration, size, scattering length density) are adjusted.	This approach uses mathematical transformations (e.g. Fourier Transforms) to convert the measured scattering data in reciprocal-space (i.e. in Q-space) into a function in real-space. Typical outputs are density correlation functions, volume fraction distributions, and size distributions.	This approach uses iterative optimisation to match the calculated scattering from assemblies of spheres or from a 3D 'shape envelope function' to the measured scattering data. Each iteration the number and/or position of the spheres, or the curvature of the envelope function, is adjusted.	This approach uses iterative optimisation in combination with Monte Carlo (MC) and/or Molecular Dynamics (MD) techniques or RRT searches to match a calculated 'atomistic level' structure for the scattering objects to the measured scattering data.	Other approaches to data analysis may involve identifying, for example: any Q-dependencies in the measured data, particular patterns in the Q-values of any peaks present, asymptotic extrapolations, calculation of the integral under the measured data (the 'invariant'), or the intensity at Q=0.
This approach: - is easy to learn; - is good for well-defined scattering objects (e.g. nanoparticles, micelles, vesicles, polymer coils, etc) or combinations of these; - works best if some a priori information about the scattering objects is available (e.g. shape, approximate size, etc) to guide initial parameter values; - is generally quick, especially for 1D data (i.e. I(Q) vs Q); - can work on 2D data (i.e. I(Qx,Qy) vs Qx & Qy); - can allow co-optimisation of data of different contrasts (or even of SAXS and SANS data); - can allow for magnetic-SANS;	This approach: - is typically used to analyse data from (semi-)crystalline polymers, adsorbed polymers, voids/pores in solid materials, or nucleating systems; - is model-independent; - needs high-quality data (i.e. good signal-to-noise) to transform; - needs data over a wide-Q-range (at least 3 decades);	This approach: - requires an investment in learning to use it well; - is well developed for solution structural biology, but has been used to simulate micelles, etc; - does not require a starting structure; - does not require any force fields; - ignores any chemistry and physics (there are no chemical bonds, for example); - can allow for hydration layers;	This approach: - requires an investment in learning to use it well; - is presently really only developed for solution structural biology, though a goal is to extend it to more generic soft matter systems; - requires an 'atomistic' starting structure (e.g. from the PDB or a MD trajectory); - requires suitable force fields; - is compute-intensive (though there are some cloud-based implementations); - preserves the chemistry and physics of the structure; - can allow for hydration layers;	This approach can provide: - fractal dimensions; - the type of ordering (fcc, bcc, hcp, etc) in the sample; - the specific surface area of the sample (S/V); - persistence lengths; - osmotic compressibilities;
Software packages for this include: - SasView - SASfit - Scatter - Irena - WillItFit	Software packages for this include: - (G)IFT* - Corfunc* - MAXE - PRINSAS** - McSAS included in SasView; *obsolete	Software packages for this include: - ATSAS Suite - FoXS -Shape2SAS	Software packages for this include: - SASSIE (incl. SCT)* - MultiFoXS - Shapespyer *also see CCP-SAS	Software packages for this include: - various (incl. spreadsheets)